
実践編!Haskellらしいアプリケーション開発。まず型を定義すべし【第二言語としてのHaskell】
トランプを使った有名なゲーム「ブラックジャック」の手札の値を計算をするアプリケーションを書きながら、Haskellによるプログラミングの中心となる「型を定義し、その型を利用した関数を書く」ことを実践してみましょう。
こんにちは。Haskell-jpの山本悠滋(igrep)です。
Haskellでプログラミングを始めるのに最低限必要となるものを「Haskellらしさって?「型」と「関数」の基本を解説!」という記事でお話しました。
その際に「Haskellによるプログラミングの大きな部分を占めるのは、問題に合わせた型を自分で考えて定義し、その型を利用した関数を書くこと」 と宣言しましたが、実践するところまでは踏み込みんでいません。
この記事では、実際にアプリケーションの一部を書きながら、「型を定義し、その型を利用した関数を書く」ことを実践してみましょう。 その途中で、Haskellのさまざまな機能や、関数の組み立て方も学んでいきます。
題材としては、トランプを使った有名なゲーム、「ブラックジャック」の手札の値を計算をする関数を作ります。
- ブラックジャックにおける手札の数え方
- 型を定義して、カード(Card)を作る
- 定義したCard型を生かして、都合のよい手札の合計値を求めるには
- Card型を使った関数を作る その1 toPoint関数
- toPoint関数をいじって、パターンマッチの特徴を知る
- Card型を使った関数を作る その2 sumHand関数
- まとめと次回予告
ブラックジャックにおける手札の数え方
ブラックジャックは、最初に配られる2枚の手札をもとに、追加のカードを1枚ずつ要求していって、手札の合計を21になるべく近づけていくゲームです。追加のカードによって手札の合計が21を越えてしまったら負けです。 手札の合計を計算するときは、次のようなルールに従ってカードを数えます。
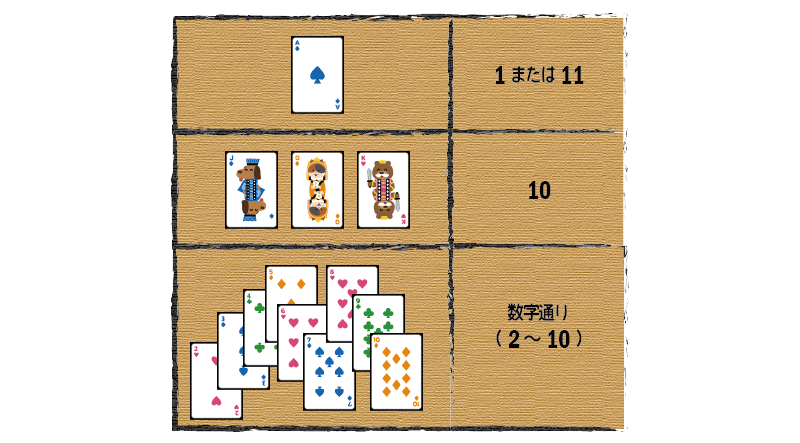
ブラックジャックにおける手札の数え方
今回紹介するソースコードは、すべて{$_2}Yuji Yamamoto / haskell-as-second-language-blackjack · GitLabに公開してあります。 hspecを使ったテストコードのほか、stackを使ったHaskellで書かれたプロジェクトのサンプルにもなっていますので、参考にしてみてください。
型を定義して、カード(Card)を作る
手始めに、ブラックジャックのカードを表す型を定義しましょう。 ブラックジャックで使うトランプのカードはジョーカーを除いた52枚ですが、今回は絵柄(ハート、ダイヤ、クラブ、スペード)の違いは無視し、AからKまでの13種類のカードを表現する型を考えます。
カードの種類を単純に列挙した型を考える
Haskellでは、dataというキーワードを使って、ユーザー定義型を定義できます。
dataは、Javaのようなオブジェクト指向言語でクラスを定義するのと同じような気分で使っていただいてかまいません。
詳細はこれから説明しますが、大体同じこと、あるいは比較対象の言語によってはそれ以上のことができます。
13種類のカードを表す型をdataで定義するには、たとえばこのようにします。
data Card = A | N2 | N3 | N4 | N5 | N6 | N7 | N8 | N9 | N10 | J | Q | K deriving (Eq, Show)
data Card = ...で始まっていることから察せられるとおり、この例ではCardという名前の型を宣言しています。
型の名前Cardの先頭Cが大文字になっている点に注意してください。
原則として、型の名前はアルファベット大文字で始めなければならないことになっています。
その次の行では、Card型がどのような値を取り得るのかを表すために、値コンストラクターを列挙しています。
縦棒(|)は、「または」と読み替えてください(or演算子(||)などと由来は同じです)。
上記の例は、「型Cardは、AまたはN2またはN3またはN4または(... 長いので省略 ...)またはQまたはKという値を取り得る」という意味になります。
上記の定義でやっていることは、Javaのような言語でenumを定義しているのと同じようなものだといえます。
「AまたはN2またはN3またはN4または(... 長いので省略 ...)またはQまたはK」という値をとるenumを定義しているのと同等なのです。
上記のコードをblackjack.hsというファイルに保存して、このCard型が正しく定義できていることを確認してみましょう。
stack ghciコマンドでGHCiを起動した後、:l blackjack.hsとして、作成したファイルを読み込んでください。
$ stack ghci > :l blackjack.hs
エラーなくファイルを読み込めたら、定義した型の値を入力して何が起こるか確認してみましょう。
> A A > N2 N2
dataで宣言したCardの値であるAやN2を入力してもエラーにならないことから、GHCiがCard型の値を認識できていることが分かります。
とはいえ、今のところ入力した値が表示されるだけなので、本当に定義できているのか実感が分かないかもしれません。
そういう場合は、いったん:qでGHCiを終了させた後、再起動してもう一度AやN2などを入力してみてください。
GHCiがAやN2などを認識できず、エラーになるはずです。
型が定義できたことをGHCiのコマンドで確認する
前回の復習になりますが、:tや:iといったGHCiのコマンドを使ってCard型が定義できたかを確認することもできます(やはり復習になりますが、:lや:qと同様、これらはGHCi専用のコマンドです。Haskellの文法とは直接関係がないのでご注意ください)。
:tコマンド(:typeの略)は、前回説明したとおり、指定した値がどんな型の値か教えてくれるコマンドです。AやKに使うと、ちゃんとCard型の値となっていることが分かりますね。
> :t A A :: Card > :t K K :: Card
:iコマンド(:infoの略)は、値に対して使うだけでなく、型に対しても使える便利なコマンドでした。
型の名前を与えると、型の定義を詳しく見ることができます。
> :i Card data Card = A | N2 | N3 | N4 | N5 | N6 | N7 | N8 | N9 | N10 | J | Q | K -- Defined at blackjack.hs:95:1 instance [safe] Eq Card -- Defined at blackjack.hs:96:35 instance [safe] Show Card -- Defined at blackjack.hs:96:39
先ほどblackjack.hsに保存したCard型の定義が、ほぼそのまま出てきました。意図した通りにCard型ができているようです
(「instance [safe] Show Card」などといった部分が気になるかもしれませんが、申し訳なくも今回は割愛させていただきます)。
【コラム】カードの型を生の整数で表すのではだめなの?
トランプの大半のカードは数字のカードなのですから、Card型を自分で定義したりせず、単純に整数(Int型など)で表すのではだめなのでしょうか。
そのほうが、あとで合計を計算するときにも楽そうです。
しかし、Intでカードを表すことには、次のような問題があります。
- ブラックジャックのルール上、
Aは1点とも11点とも数えることができる。単なるIntではこれを表現できない - カードを
Intで表現してしまうと、Intで表せそうなほかの値と紛らわしくなる- ある変数に整数
1が代入されていたとき、それが手札を計算した合計の「1」なのか、それとも手札を計算する前のカードAを表す「1」なのかを区別できない - ほかの意味でも整数の
1を使うことがありうる。たとえば、オンライン対戦やコインをかける機能があれば、「1」でユーザーのIDを表したり、ユーザーがベットしたコインの枚数を表したりするかもしれない
- ある変数に整数
カードにはカードのための型を割り当てたほうが、こうした紛らわしさを軽減し、間違えを少なくできるのです。
2~10のカードだけ、パラメータを1つとる別の型にしよう(直和型)
:iコマンドでCard型の情報を表示させると、型の定義が次のように表示されました。
> :i Card data Card = A | N2 | N3 | N4 | N5 | N6 | N7 | N8 | N9 | N10 | J | Q | K
この結果を見ると、この定義の「N2 | N3 | N4 | N5 | N6 | N7 | N8 | N9 | N10」という部分がちょっと冗長に思えますね。
今回のカードの仕様では、2から10までのカードは同じ値の整数と1対1に対応しています。
これらをまとめてIntに関連付けて表せれば、Card型の定義はかなりすっきりしそうです。
ただし、見かけ上の区別があるJ、Q、Kと、点数計算のルールがほかのカードと異なるAは、Intに関連付けて表すわけにはいきません。
A、J、Q、K以外の値だけをIntに関連付けて表すことができる、より直感的で実態に合うカードの型が作れないものでしょうか。
これをそのまんま実現するのが、Haskellの直和型と呼ばれる機能です。
直和型を使ったCard型の定義はこうなります。
data Card = A | N Int | J | Q | K deriving (Eq, Show)
Card型が取り得る値コンストラクターを縦棒|を用いて列挙している点は、先ほどの定義と同じです。
A、J、Q、Kの4つの値コンストラクターについても、何も変えていません。
しかし、N2 | N3 | N4 | N5 | N6 | N7 | N8 | N9 | N10と長ったらしかった部分が、N Intとまとめられていますね。
このN Int、一体何を表しているのでしょうか。ほかの値コンストラクターとは異なり、Nの後ろにIntが付いた形をしていますが、実はこのN Intも値コンストラクターです。
まず、N Intの先頭にあるNは、この値コンストラクターの名前です。型の値コンストラクターに名前があるのは、これまでに出てきた値コンストラクタ―のAやJ、N1などと同じです。
そして、Nの後ろに付いているIntは、「値コンストラクターNの引数の型」です。
よくあるオブジェクト指向言語において「フィールド」とか「プロパティ」と呼ばれているもの、というとピンとくる人もいるかもしれませんね。
ここで重要なのは、このInt型の引数を保持できるのは値コンストラクターがNのときだけという点です。
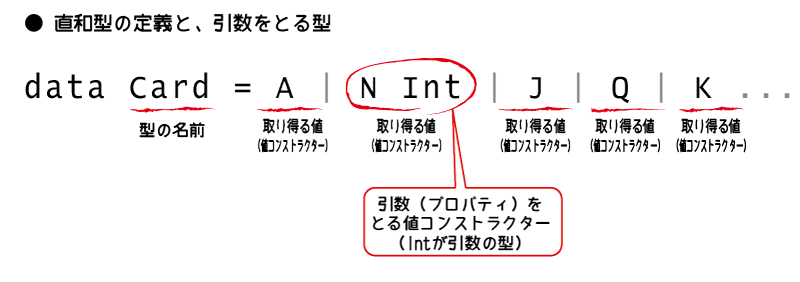
値コンストラクターを使った直和型の定義
値コンストラクターの引数について、もう少しだけ別の例でも説明してみましょう。
データ型の定義方法の説明では、名前Stringと年齢Intの人物を表現した、次のようなPerson型の定義がよく使われます。
data Person = Person String Int
同名なので紛らわしいですが、型の名前がPersonで、その唯一の値コンストラクタ―がPerson String Intです。
その値コンストラクターの名前がPersonで、スペースで区切られた残りのString Intは、値コンストラクターPersonの引数の型、言い換えると、プロパティの型を表しています。
プロパティに名前が付いておらず、型だけ指定して定義されていることに驚いた人も多いでしょう。Haskellでは、このように、値コンストラクターに名前を持たない引数を定義できるのです(名前をつける方法もありますが、今回は割愛します)。
しかし、名前を持たないプロパティに一体どうやってアクセスすればいいのでしょう?
ほかの言語であれば、プロパティのアクセスにはperson.nameやcard.numberなどとするところですが、名前がないのでそれができません。
実は、Haskellでは「パターンマッチ」という機能を使って値コンストラクタ―の引数を利用します。詳細は後ほど説明しますので、お楽しみに。
Card型の話に戻ります。新しいCard型の定義では、A、N、J、Q、Kの5つのコンストラクターのうち、Nだけがカードの番号を表すInt型のプロパティを持つようにしました。
これでCard型がきちんと定義できているかどうか、新しいCard型の定義でblackjack.hsを書き換えてからGHCi上で試してみましょう。
> :l blackjack.hs > :i Card data Card = A | N Int | J | Q | K instance [safe] Eq Card instance [safe] Show Card > A A > :t A A :: Card
:iコマンドの結果表示は、data Cardの部分が変わった以外、今のところ変化はありません。定義を変えていない値コンストラクターAやKもそのまま使えます。
では、Nはどうでしょう?
> N <interactive>:5:1: error: ・ No instance for (Show (Int -> Card)) arising from a use of ‘print’ (maybe you haven't applied a function to enough arguments?) ・ In a stmt of an interactive GHCi command: print it
そのままGHCiに入力するとエラーになってしまいました。:tで型を見るとどうなるでしょうか?
> :t N N :: Int -> Card
Int -> Cardという型が返ってきました。これは、前回も紹介した関数型です。
この場合、「Int型の値を受け取ってCard型の値を返す関数」という意味になります。
そう、NはInt型の値(整数)を受け取る関数となったのです!
残念ながらGHCiでは関数を表示させることができません(これは、どちらかというとHaskellの都合です。詳しくは、英語ですがHaskellWikiの「Show instance for functions」をご覧ください)。
先ほどのエラーは、「関数を入力しても、コンソールには表示できないよ」というエラーだったのです。
今度は、Nに引数を指定し、関数として使ってみましょう。
関数を呼び出すには、前回の記事でbmi関数を使ったときのように、関数名と引数をスペースで区切って並べるだけでしたね。
> N 2 N 2
今度はエラーになりません。 では、型はどうなっているでしょう?
> :t N 2 N 2 :: Card
「N 2はCard型である」という結果が返ってきました。
このように、Card型の値コンストラクターNは、関数としてIntを受け取ってはじめてCard型の値となるのです。
これは、Javaなどのオブジェクト指向言語でコンストラクターに引数を与えているのと同じようなものです。
値コンストラクタ―でも、与えた引数がそのままNのプロパティーとなります。
そして、AやJ、Q、KがIntを受け取らずにCard型となっていたことから分かるとおり、カード番号としてIntを受け取るのはNだけなのです。
以上により、数字のカードだけに整数を関連付けて型を定義するという要件を満たすことができました。
derivingで、型クラスに属する型(インスタンス)を自動で定義する
ここまで、Card型を例として、Haskellにおいて新しい型を作成する方法を紹介しました。
しかしながら、新しい型を定義する構文について、まだ紹介し切れていない箇所があります。
先ほどのCard型の宣言の末尾にあるderiving (Eq, Show)という箇所です。
data Card = A | N Int | J | Q | K deriving (Eq, Show)
deriving (Eq, Show)というのは、Card型をEq型クラスとShow型クラスに所属させる(Card型をEq型クラスとShow型クラスのインスタンスにする)ために必要な宣言です。
型クラスは、前回の記事で説明したとおり、「同じような特徴(振る舞い)を持った型を、ひっくるめて扱えるようにする仕組み」です。
Num型クラスが「足し算、かけ算、引き算ができる型」をまとめた型クラスであったり、Fractional型クラスが「それらに加えて割り算ができる型」をまとめた型クラスであったりしたように、それぞれの型クラスには、それぞれがまとめた型に共通する特徴があります。
では、Eq型クラスとShow型クラスにはどんな特徴があるのでしょう?
Eq型クラスとShow型クラスの特徴は非常によく使われるので、自分で定義する型にはほとんどいつもderiving (Eq, Show)を付けて宣言したくなるはずです!
2つの値が「等しいかどうか」を比較できるような型にするには(Eq型クラス)
Eq型クラスは、2つの値が「等しいかどうか」比較できる型をまとめる型クラスです。
具体的には、おなじみの==で2つの値が比較できるような型ということです。
IntやChar、String、リストなど、これまでの説明に出てきた型は、関数型とIO型を除いてすべてEq型クラスに所属しています。
GHCiで確かめてみましょう。
> 'a' == 'a' True > True == True True > 3 == 2 False > "hello" == "Hello" False -- リストやタプルを比較する際の「==」は、すべての要素を「==」で比較して、 -- すべてが等しい場合のみTrueを返す > ('a', True) == ('c', True) False > [1, 2, 3] == [1, 2, 3] True
ちなみに、Haskellの==にはほかのプログラミング言語にはないちょっと変わった特徴があって、同じ型同士の値でないと比較ができません。
たとえば、次のように真偽値Trueと"True"という文字列を比較しようとすると型エラーになります。
> True == "True" <interactive>:9:9: error: • Couldn't match expected type ‘Bool’ with actual type ‘[Char]’ • In the second argument of ‘(==)’, namely ‘"True"’ In the expression: True == "True" In an equation for ‘it’: it = True == "True"
ちょっと厳しく思えるかも知れませんが、ほかのプログラミング言語でも、暗黙の型変換が働くようなケースを除けば、違う型の値による比較はFalseを返すことになるでしょうし、通常はやる必要がないでしょう。
型が曖昧になることを嫌うHaskellでは、暗黙の型変換も違う型の値の比較も認めていないというだけのことです。
値を文字列として表示できるような型にするには(Show型クラス)
Show型クラスに属する型は、showという関数によって、値を文字列に変換できます。
Show型クラスについても、IntやChar、String、リストなど、前回紹介した型は、関数型とIO型を除いてすべて所属しています。
こちらもGHCiで確かめてみましょう。
> show 'a' "'a'" > show False "False" > show "12345" "\"12345\"" > show 12345 "12345" > show 139.17 "139.17" > show ('c', True) "('c',True)" > show [3, 2, 1] "[3,2,1]"
文字列"12345"をshowした場合には、"12345"という文字列そのものではなく、ダブルクォートで囲った"\"12345\""(ダブルクォートがバックスラッシュでエスケープされていることに注意)が出力されました。
このことから分かるように、show関数によって作成される文字列は、ほかの型の値をshowした文字列から区別できるように作られています。
たとえば、上記のshow "12345"の結果とshow 12345の結果を比較してみると、型が違うと違う文字列が返ってくるように作られていることが分かります。
そうした意味では、Rubyでいえばto_sメソッドよりもinspectメソッド、Pythonでいえばstr関数よりもrepr関数に近い挙動です。
したがって、show関数は、どちらかというとデバッグで値の中身を見るために使用するのがおすすめです。
【コラム】GHCiの表示はshow関数の変換結果
実は、GHCiで入力した式をコンソール上に表示する際にも、内部ではshow関数を使用しています。
入力した式の値を、show関数で文字列に変換することで表示しているのです。
なので、下記のように、Show型クラスに属さない関数型の値を入力するとエラーになってしまいます。
> (+)
<interactive>:15:1: error:
• No instance for (Show (a0 -> a0 -> a0))
arising from a use of ‘print’
(maybe you haven't applied a function to enough arguments?)
• In a stmt of an interactive GHCi command: print it
> not
<interactive>:16:1: error:
• No instance for (Show (Bool -> Bool))
arising from a use of ‘print’
(maybe you haven't applied a function to enough arguments?)
• In a stmt of an interactive GHCi command: print itこうした特徴のため、自分で定義した型をShow型クラスのインスタンスにしておくと、定義した型の値を返す関数をGHCiで試したとき、どんな値が返ったかを確認するのが簡単になります!
そして、以下で説明するように、deriving Showとするだけでそれがタダで手に入るのです。
Eq型クラスとShow型クラスの性質を手軽に得る
この項の冒頭で説明したように、deriving (Eq, Show)と書くことによって、Card型をEq型クラスとShow型クラスに自動で所属させる(Card型をEq型クラスとShow型クラスのインスタンスにする)ことができるのでした。
これらを自動で行うということは、Card型の値を==で比較する方法や、show関数でCard型の値を文字列に変換する方法を、自動で定義するという意味です。
具体的にどのように==で比較したり、show関数で文字列に変換したりするのでしょうか?
実は、Card型がshow関数でどのような文字列に変換されるかは、すでに知っています。
GHCi上で次のように入力したときのことを思い出してください。
> A A > N 2 N 2
値コンストラクターAを入力したときも、引数を与えた値コンストラクターN 2を入力したときも、いずれも入力した文字列がそのまま出力されました。
そして、show関数は、GHCiで入力した式をコンソール上に表示する際に内部で使用されています。
ということは、上記の実行例で表示された結果は、Card型の値をshow関数で変換した際の文字列だということですね。
試しにshow関数を実行してみると、そのことがよりはっきり分かります。
> show A "A" > show (N 7) -- 丸カッコで囲むのを忘れないでください! "N 7" > show J "J" > show Q "Q" > show K "K"
このように、deriving Showして定義された型のshow関数は、値コンストラクターや、値コンストラクターに渡した引数(値コンストラクターのプロパティ)がそのまま文字列として返るように定義されます。
これは、先ほども触れた「デバッグの際、値の中身を見るために使用する」という用途にもマッチしていると言えるでしょう。
出力された文字列をそのままソースコードに貼り付けて再利用するといった用途にも向いています。
Card型のEq型クラスの実装についても、GHCiで試してみるとよく分かるでしょう。
-- 同じ種類の値コンストラクターだからTrue > A == A True -- それ以外はすべてFalse > A == J False > A == K False > J == J True > A == N 3 False -- 引数(プロパティ)を持つ値コンストラクターも、 -- もちろん違う種類の値コンストラクターだとFalse > N 3 == K False -- 同じ種類の値コンストラクターでも、 -- 渡した引数が同じ値(「==」で比較される) -- でなければFalse > N 3 == N 2 False -- 値コンストラクターの種類と -- 渡した引数が同じ値になって初めてTrue > N 3 == N 3 True
このように、deriving (Eq, Show)して作られた==関数の実装は、両方とも非常に直感的なものとなっています。
Eq型クラスとShow型クラスのユースケースは想像以上に多くあります。
たとえば、hspecなどの自動テストフレームワークにおいて期待した結果と実際の結果が等しいかどうかを確認したり、等しくなかった場合に実際の結果を表示したりするには、対象の型がShow型クラスやEq型クラスのインスタンスである必要があります。
そのため、みなさんが新たに定義した型には、特別な事情がある場合を除いて、なるべくderiving (Eq, Show)とおまじないのように書いておくことをおすすめします。
ちなみに、「特別な事情がある場合」とは、もともとEq型クラスにもShow型クラスにも属していないIO型や関数型の値をプロパティとして持つ型を定義する場合などが該当します。
定義したCard型を生かして、都合のよい手札の合計値を求めるには
Card型が定義できたところで、その型の特徴を利用し、手札の合計を求める関数を書いていきましょう。
まず、そのような関数の型を考えます。
手札は複数のCardですから、手札の型はCardのリスト[Card]でいいでしょう。
手札を計算した合計のほうは、整数になるので、Intで表現しましょう。
この関数の名前は、手札(hand)を合計するので、そのままsumHandとしましょう。
以上をまとめると、手札の合計を求める関数sumHandは、Cardのリストを受け取ってIntを返すものになりそうですね。
そのことを型で表すと、こうなります。
sumHand :: [Card] -> Int
このように、関数の名前の後ろのコロン2つ::以降で関数の具体的な型名を示したものを、関数の型宣言といいます。
Haskellで関数を定義するときは、型宣言を1行めに明記することで、「その関数がプログラムのどこに影響を与えるのか」の範囲を示します。
関数の定義に型宣言が付いているおかげで、
- 入出力処理を行う関数か(つまり、プログラムの外の世界に影響があるか)?
- 暗黙に共有されている変数を読み書きする関数なのか(プログラム内で広範囲に共有されている変数に影響があるか)?
- エラーを発生させて後続の処理を強制終了させる関数なのか(プログラムのフローに影響するか)?
- はたまた、単純に値を返すだけの関数か(戻り値を受け取る変数に影響するか)?
といったことを、関数の型だけで明示できるのです(実際には、デバッグなどのために作られた例外もあります)。
【コラム】型宣言は常に必要か?
静的型付け言語に抵抗がある方は、わざわざ型宣言を書くことが面倒くさいなと感じられるかもしれません。
実際、Haskellには強力な型推論の機能が備わっているので、多くの場合は型をわざわざ書く必要はありません(前回の記事のbmi関数でも、型宣言はあえて省略していました)。
それでも、型宣言をすることで関数の型を明示すれば、コンパイラーが自動で正しさを証明してくれた信頼性の高いドキュメントになります。 みなさんも、分かりやすさのために、関数の定義では積極的に型を明示することをおすすめします。
続いて具体的な関数の中身を考えましょう。 型宣言の下に、関数の定義を書いていきます。 関数を定義するときは、関数名と引数名を書いて、イコール記号の後ろに具体的な処理を書いていくのでしたね。
sumHand :: [Card] -> Int sumHand cards = ...
「...」の部分は、手順として考えると、以下のようなアルゴリズムになるでしょうか?
- 手札の各カードを、取り得る値に変換する
- 取り得る値の組み合わせすべてについて、それぞれ合計を求める
- 合計のうち、バストしない(合計が21を超えない)もののみを選ぶ
- バストしない合計が1つでもあった場合、その中から最も高い値の合計を選んで返す
- バストしない合計が1つもない場合(どの合計もバストしてしまう)、合計の中から適当なものを選んで返す(ここでは「リストの先頭」を選ぶものとします)
ブラックジャックには、「Aは1または11のどちらでも都合のよいほうで計算できる」というルールがあるので、それに対応するため、まずは手札の各カードを可能性のある値のリストに変換しています。
あとは、その値の組み合わせのうちで都合がよい値(つまり、21にもっとも近く21を越えない値)を選び出すための手順です。
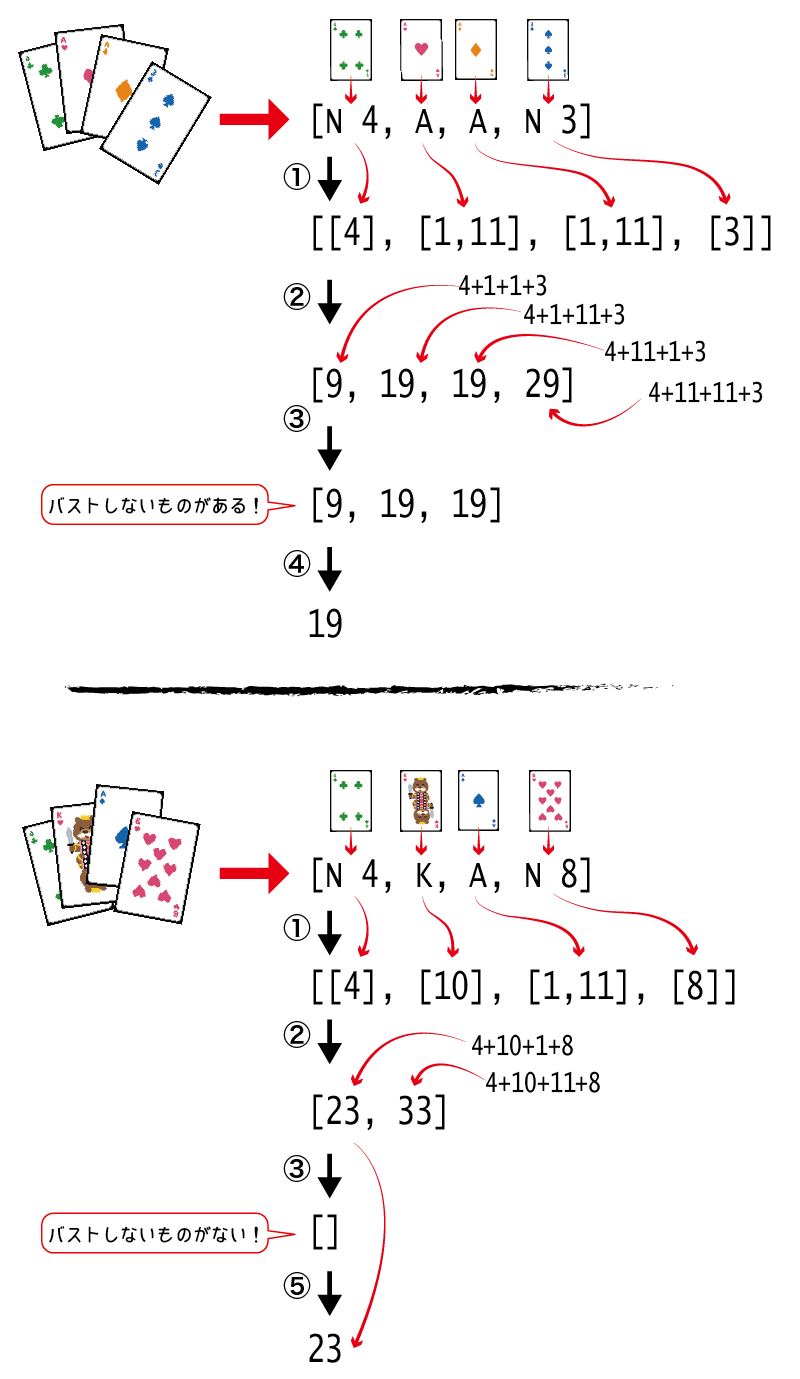
sumHandのアルゴリズム
この関数の目的は、あくまでも「手札の合計を計算する」ことなので、上記の手順だけで要件はすべて満たせそうです。 入出力処理などは一切必要ありませんね。 そこで、「値を受け取って返す以外には何もしない」純粋な関数のみを組み合わせることで、目的の関数を作っていくことにします。
以降の解説では、いきなりsumHandを定義していくのではなく、まず上記のアルゴリズムの1つ目の手順「手札の各カードを、取り得る値に変換する」を担う関数を定義します。
そのため、書きかけのsumHandの定義は、文字通りundefined(未定義)としておいてください。
sumHand :: [Card] -> Int sumHand cards = undefined
undefinedは、関数や変数の中身が未定義な場合に使用する、特別な値です。
ちょうどJavaにおけるnullのように、どのような型の値の代わりにもなれるので、強引に型エラーを回避することができます。
ただし、undefinedなままでsumHandを使用すると実行時に必ずエラーになってしまうので、くれぐれもご注意ください。
undefinedは、あくまでも「後で書く」という意図を伝えるためだけに使用してください。
Card型を使った関数を作る その1 toPoint関数
「Card型を変換して取り得る値にする関数」の名前は、toPointとしましょう。
いきなり答えから見せてしまいますが、下記がtoPointのHaskellでの定義です。
toPoint :: Card -> [Int] -- 関数の型の宣言 toPoint A = [1, 11] -- Aの場合は1と11を取り得る toPoint (N n) = [n] -- 通常の数字のカードであれば、カードに書かれた数字のみを取り得る toPoint _ = [10] -- そのほかの場合は10のみをとる
前回定義したbmi関数では使用しなかった構文をいくつか使用しているので、これらを丁寧に解説していきます。
関数toPointの型宣言
1行めは、関数の型宣言です。
toPoint関数の場合は、「Card型の値を受け取り、Intのリスト[Int]を返す関数」という意味になります。
toPoint :: Card -> [Int] -- 関数の型の宣言
関数の本体をパターンマッチで定義する
関数の型宣言より下の3行が、実際の関数の定義です(ちなみに、関数の型宣言と定義は、同じファイル内にあれば離れた箇所にあっても問題ありません)。
toPoint A = [1, 11] -- Aの場合は1と11を取り得る toPoint (N n) = [n] -- 通常の数字のカードであれば、カードに書かれた数字のみを取り得る toPoint _ = [10] -- そのほかの場合は10のみをとる
toPoint ... = ...と書かれた行が3つもあることから、toPoint関数の定義が3つもあるように見えて、最初はちょっと変に思えるかもしれません。
これが、先ほど名前だけ登場したパターンマッチの構文です(等価な書き方がほかにもいくつかあるので、そのうちの1つです)。
上記の定義では、パターンマッチを使うことで、Card型が取る値に応じて返す値を変えるように振り分けています。
1行めから見ていきましょう。
toPoint A = [1, 11] -- Aの場合は1と11を取り得る
この行は、「第1引数として受け取った値が、Card型の値コンストラクターのうちAであれば[1, 11]を返す」という意味です。
toPoint関数の型宣言では「Intのリスト[Int]を返す」としましたが、確かに[1, 11](1と11が入ったリスト)を返していますね。
その下の2行は、受け取った引数がAでなかった場合に使用されます。
toPoint (N n) = [n] -- 通常の数字のカードであれば、カードに書かれた数字のみを取り得る toPoint _ = [10] -- そのほかの場合は10のみをとる
このように、値コンストラクターの種類に応じて返す値を振り分けるというのが、パターンマッチの用途の1つです。
手続き型の言語でいえば、次のようなif文と似たことをしているといえるでしょう(下記は特定の言語の構文ではなく、疑似コードです)。
function toPoint(x) {
if (x == A) {
return [1, 11]
} else if (...) {
...
}
}
あらためて、定義の2行めを見ていきましょう。
2行めでは、値コンストラクターがNの場合に返す値を定義しています。
toPoint (N n) = [n] -- 通常の数字のカードであれば、カードに書かれた数字のみを取り得る
返す値は[n]、つまりnだけを含むリストとなっていますが、さてこのnはどこからきた何の値でしょう?
答えは、引数の箇所に書かれている(N n)のnです。
これはまさに、値コンストラクターNに与えた引数です。
例えばN 2であればnは2となりますし、N 5であればnは5となります。
パターンマッチは、このように、値コンストラクターの種類ごとに分岐するだけでなく、値コンストラクターに与えた引数(プロパティ)を取り出すという用途にも使えます。 前に「値コンストラクターの引数はプロパティのようなものだが、名前がなくてもいい」と説明しましたが、これで、プロパティに名前がなくてもアクセスできることが分かりましたね(ちなみに、名前を持っているプロパティでも同じ方法でアクセスできます)。
定義の3行めの説明がまだ終わっていませんが、こここでいったん動作を確認してみましょう。
ここまでに書いた関数をblackjack.hsに追記し、GHCiから:l blackjack.hsで再び読み込んで実験してみましょう。
$ stack ghci > :l blackjack.hs > toPoint A [1,11] > toPoint (N 1) [1] > toPoint (N 9) [9]
仕様通り、Aを受け取れば1と11が返り、Nを受け取ればNに渡した整数がそのまま返ることが確認できました。
【コラム】関数呼び出しにしないためのカッコ
(N 1)のように、Nの関数呼び出しを丸カッコで囲むのを忘れないでください。
丸カッコで囲まずtoPoint N 3のように呼び出してしまうと、下記のようにエラーになります。
> toPoint N 3
<interactive>:2:1: error:
• Couldn't match expected type ‘Integer -> t’
with actual type ‘[Int]’
• The function ‘toPoint’ is applied to two arguments,
but its type ‘Card -> [Int]’ has only one
In the expression: toPoint N 3
In an equation for ‘it’: it = toPoint N 3
• Relevant bindings include it :: t (bound at <interactive>:2:1)
<interactive>:2:9: error:
• Couldn't match expected type ‘Card’
with actual type ‘Int -> Card’
• Probable cause: ‘N’ is applied to too few arguments
In the first argument of ‘toPoint’, namely ‘N’
In the expression: toPoint N 3
In an equation for ‘it’: it = toPoint N 3これは、Haskellの仕様上、toPoint N 3という関数呼び出しは、「toPoint関数に2つの引数Nと3を渡した」という意味で解釈されてしまうからです。
慣れないうちはしばしば間違えてしまうので、型エラーが出た際は真っ先に疑うといいでしょう。
特に、上記のようにexpected typeかactual typeのどちらかが関数(Int -> Cardのように矢印が含まれている)で、もう一方が関数でない型の場合、特にその可能性が高いです。
Cardを直和型にしたことの効能
Card型では、5つのコンストラクターのうち、Nだけがカードの数字を表すInt型のプロパティを持っているのでした。
そのため、パターンマッチでほかの値コンストラクターから値を取り出そうとしても、当然エラーになります。
それも試してみましょう。
関数の定義でAのカードに対応する下記の行を……
toPoint A = [1, 11]
次のように書き換えてみてください。
toPoint (A n) = [1, 11]
それから、再度:l blackjack.hsしてみましょう。
> :l blackjack.hs [1 of 1] Compiling BlackJack ( blackjack.hs, interpreted ) blackjack.hs:230:10: error: • The constructor ‘A’ should have no arguments, but has been given 1 • In the pattern: A n In an equation for ‘toPoint’: toPoint (A n) = [1, 11] Failed, modules loaded: none.
丁寧なエラーメッセージが出ました。エラーメッセージを日本語に訳すと以下のような感じでしょうか。
- コンストラクター 'A' は引数を持っていないはずなのに1個与えています。
- 発生したパターン: A n
'toPoint' 関数における等式「toPoint (A n) = [1, 11]」にて発生。
文字通り、「引数を持っていない値コンストラクターに引数を渡した」ことを教えてくれています。
これは、直和型を使って、値コンストラクターがNのときだけプロパティを保持できるようにしたことによる効果です。
直和型をサポートしない言語でカードを単純に表現しようとすると、「数字を取らないA、J、Q、Kの各値では、プロパティとしてnullを代入する」といった対応をすることになるでしょう。
その結果、数字を取らない値から間違えて数字を取得しようとしてしまい、意図せずnullを参照してしまう原因を作ってしまうかもしれません。
Haskellでは、直和型のおかげで、本当に必要なケースのみにプロパティを付与できます。 それにより、無駄なコードを排除できるだけでなく、そうした間違えの可能性を未然に排除できるのです。
「何でもよい」にマッチさせるには
さて、toPoint関数の定義も残り1行です。
ここまで触れていなかった下記の行について説明しましょう。
toPoint _ = [10] -- そのほかの場合は10のみをとる
Aと数字が書かれたカードを除くと、残っているカードの型はJ、Q、Kです。
そのことから察せられるとおり、これはtoPoint関数がAでもNでもなくJ、Q、Kのいずれかを受け取った場合に対応する定義です。
その場合の返す値は、[10](10だけが入ったリスト)ですね。
GHCi上で試してみましょう。
> toPoint J [10] > toPoint Q [10] > toPoint K [10]
でも、どうしてこんな結果が得られるのでしょうか?
toPoint _ = [10]という定義のうち、toPointが関数名、イコールより後ろの[10]が返り値を表しているのは分かると思いますが、イコールの左側に出てくるアンダースコア_が謎ですよね。
このアンダースコアは、仮引数です。
「仮」なので、アンダースコアでないといけないわけではなく、適当なアルファベットの小文字でも動きはします。
試しに、定義を下記ようように書き換えて:l blackjack.hsし、toPoint Jなどの結果を試してみてください。
動作は変わらないはずです。
toPoint n = [10] -- そのほかの場合は10のみをとる
パターンマッチで値コンストラクターごとに処理を振り分けるとき、仮引数がアルファベット小文字またはアンダースコアで始まる識別子の場合には、(引数として宣言した型に対する)任意の値コンストラクターにマッチするようになります。 これをワイルドカードパターンと呼びます。
(ちなみに、先ほどのtoPoint (N n)の定義で使用したnも任意のIntにマッチするワイルドカードパターンです。そして、前節で定義したbmi関数の仮引数height、weightも、それぞれ任意の値にマッチするパターンです。)
では、筆者はなぜこの仮引数の名前をアルファベット小文字ではなく、あえてアンダースコアにしたのでしょう? 実は、アンダースコアが名前の先頭についている仮引数や変数は、仕様上ちょっと用途が変わっていて、「関数の定義内で参照しない仮引数」として使うことになっているのです。
この用途の仮引数にアンダースコアを使うことは、GHCでも推奨しています。
試しに、GHCi上で:set -Wallと入力して警告を有効にしてから、先ほど修正したblackjack.hsを読み直してみてください。
読み直しには、下記のように、GHCiの:rコマンドが使えます。
> :set -Wall [*BlackJack] > :r [1 of 1] Compiling BlackJack ( blackjack.hs, interpreted ) blackjack.hs:232:9: warning: [-Wunused-matches] Defined but not used: ‘n’ Ok, modules loaded: BlackJack.
今度は警告(warning)が出ました。
名前がアンダースコアで始まっていない仮引数が関数の定義内で使用されていない場合、GHCは、「nを使用していないけどいいの?」と警告を出してくれるのです。
_や_nのようにアンダースコアで始まる仮引数名をつけることによって、明示的に「この仮引数は使用しない」という意図を示せます。
Haskellでプログラムを書くときは、積極的にこのような慣例に従うようにしましょう。
以上で、toPoint関数の定義は完了です。
ここまで説明したパターンマッチによる関数定義の方法を下記の図にまとめておきます。
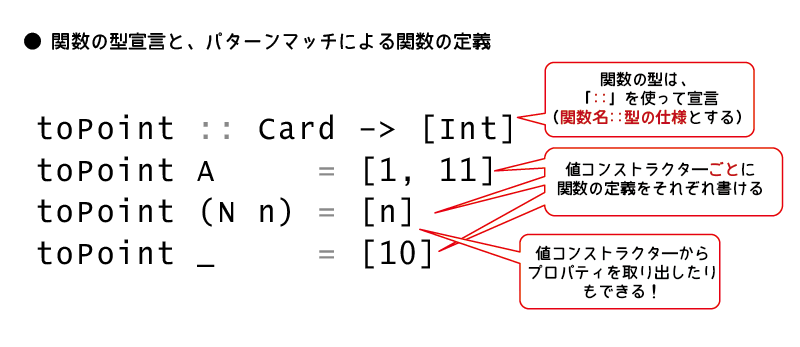
パターンマッチを使った関数の定義
toPoint関数をいじって、パターンマッチの特徴を知る
次の関数を定義する前に、toPoint関数の定義を少しいじってみることで、もう少しパターンマッチについての理解を深めましょう。
Haskellのパターンマッチがいかに間違いを防ぎ、バグの少ないプログラム作りに有効かが分かるはずです。
まず、ここまでのまとめとして、パターンマッチに関して下記の2点を押さえておいてください。
- プロパティがない値コンストラクターからプロパティを取り出そうとしても、エラーになる
- 小文字で始まる引数名を使用することで、どの値コンストラクターにもマッチするパターン(ワイルドカードパターン)を作れる
それでは、先ほどと同様にGHCiを起動して、パターンマッチまわりをいろいろ実験してみましょう。
今度は:set -Wallを入力し、警告を有効にしてからblackjack.hsを読み込んでください。
警告を有効にしなければ検出できない問題を探り出すためです。
$ stack ghci > :set -Wall > :l blackjack.hs
パターンマッチではあらゆるパターンを想定しなければならない
手始めに、toPoint関数のtoPoint _ = [10]の行を削除してみましょう。
下記のように書き換えてください。
toPoint :: Card -> [Int] toPoint A = [1, 11] toPoint (N n) = [n]
修正したblackjack.hsを読み直すと、次のような警告が出ます。
[1 of 1] Compiling BlackJack ( blackjack.hs, interpreted ) blackjack.hs:230:1: warning: [-Wincomplete-patterns] Pattern match(es) are non-exhaustive In an equation for ‘toPoint’: Patterns not matched: J Q K
「パターンマッチが網羅的でない」、すなわち抜け漏れがあるよ!という警告です。
具体的にどういうパターンを網羅していないかまで教えてくれました。
値コンストラクターJ、Q、Kを渡した場合を想定できていないようです。
ではこの、想定していない値があるtoPoint関数に、想定していない値を渡したら何が起こるでしょうか?
> toPoint K *** Exception: blackjack.hs:(230,1)-(231,19): Non-exhaustive patterns in function toPoint
Exception、すなわち例外が発生してしまいました。
想定していない値、すなわち例外的な値を与えてしまったため、文字通り例外が起きたのです。
ほかのプログラミング言語によくあるnullのような値、つまり「どんな型の値の代わりにもなる値」がないHaskellでは、パターンマッチで想定していない値を受け取った関数は、戻り値として返す値を決めることができないので、例外を投げるほかありません。
そのため、原則としてあらゆる関数は、パターンマッチで引数として取り得る値をすべて想定することが望ましいとされています。
実行時に例外が起こるとプログラムは強制終了してしまい、ユーザー体験やプログラムの信頼性を著しく損ねることになってしまいます。
できるだけ未然に防ぎたいものですよね。
上記の警告はそうしたパターンマッチの想定漏れによる例外を防ぐためのものです。
パターンマッチでは余分なパターンを想定してはいけない
今度は、toPoint関数のtoPoint _ = [10]の行をtoPoint A = [1, 11]よりも前に移動させてみましょう。
下記のように書き換えてください。
toPoint :: Card -> [Int] toPoint _ = [10] toPoint A = [1, 11] toPoint (N n) = [n]
blackjack.hsを保存した上でもう一度GHCiで読み込むと、次のような警告が出るはずです(下記に示したのは実際の出力からの抜粋です)。
> :r blackjack.hs:231:1: warning: [-Woverlapping-patterns] Pattern match is redundant In an equation for ‘toPoint’: toPoint A = ... blackjack.hs:232:1: warning: [-Woverlapping-patterns] Pattern match is redundant In an equation for ‘toPoint’: toPoint (N n) = ...
‘toPoint’: toPoint A = ...と、‘toPoint’: toPoint (N n) = ...のパターンマッチが冗長だ、という警告です。
なぜかというと、パターンマッチをしている最初の行で任意の引数にマッチする、ワイルドカードパターンを使用しているためです。
パターンマッチはほかのよくあるプログラミング言語におけるif文やswitch文などと同様に、評価するパターンを「上から順に」、すなわちパターンマッチする行を定義した順に評価します。
結果、パターンマッチの最初の行であらゆる値がワイルドカードパターンにマッチしてしまい、それ以降のパターンマッチの行が評価されないのです。
試しに書き換えたtoPoint関数を使ってみると、そのことがよく分かります。
> toPoint A [10] > toPoint (N 2) [10] > toPoint J [10]
Aを与えようとNを与えようと、toPoint _ = [10]の行で_が任意の値コンストラクターにマッチしてしまうため、[10]が返ってしまいます。
実際問題これは明らかに意図しない振る舞いでしょう。
通常のif文(あるいはif式)などと異なり、パターンマッチは、このようにマッチさせる順番を間違えた際にできてしまう、「余分なパターン」を簡単に検出することができます。
このようにパターンマッチは、処理の無駄を検出したり、取り得る値の想定に漏れがあることを検出することで、実行するまでもなくバグを検出することもできます。
(おそらく歴史的な経緯によって)残念ながら今回紹介した検出機能は警告をオンにしないと使用できませんので、みなさん実際に開発する際は必ず-Wallオプションや、警告をエラーとして扱う-Werrorを有効にして開発してください。
Card型を使った関数を作る その2 sumHand関数
前節のtoPoint関数を使って、手札の合計を計算する関数sumHandを書きましょう。
sumHandは、最初に考えたとおり、次のような型の関数です。
sumHand :: [Card] -> Int
この関数を、次のような手順で処理をするように定義したいのでした。
- 手札の各カードを、取り得る値に変換する
- 取り得る値の組み合わせすべてについて、それぞれ合計を求める
- 合計のうち、バストしない(合計が21を超えない)もののみを選ぶ
- バストしない合計が1つでもあった場合、その中から最も高い値の合計を選んで返す
- バストしない合計が1つもない場合(どの合計もバストしてしまう)、合計の中から適当なものを選んで返す(ここでは「リストの先頭」を選ぶものとします)
すでに1つ目の手順に必要な関数はtoPointとして定義ずみです。
手札に入った各カードが取り得る値の組み合わせをすべて作り、それぞれの合計を求めるには、どうすればいいでしょうか?
手続き型の言語に慣れていると、for文のような繰り返し処理をするための制御構造を使う方法が真っ先に思い浮かぶかもしれません。
ところが、実をいうとHaskellには、for文やwhile文、foreach文のような繰り返しに使う構文はないのです!(今回は紹介しませんが、実はライブラリーの関数としては存在します)
そのような繰り返しを行う関数は、基本的には再帰呼び出しを使って定義できます。 ただ、Haskellでは、コードが複雑になりがちということもあり、再帰呼び出しを直接使って関数を定義することは実践ではあまりありません。 代わりに、再帰呼び出しをベースに作った便利な関数がたくさん提供されているので、それらを使うのがHaskellでは一般的です。 それらを組み合わせるだけで、よほどのことがない限り、やりたいことは十分に実現できるのです。
ここでは、それらの便利な関数の一部を、sumHand関数を作る過程を通して紹介していきます。
map: リストの各要素に対して関数を実行し、結果をまたリストに入れる
最初に紹介するのはmap関数です。mapは、手札の各カードに対して取り得る値をそれぞれ計算するのにぴったりな関数です。
そのような「リストの各要素に対して何かする」処理を手続き型言語で書くとしたら、例えば下記のようなコードになるでしょうか?
// 結果を格納するための新しいリスト result = []; for(card in cards){ // 各カードに対して、 // toPoint関数を実行した結果を、 point = toPoint(card); // 結果を格納するリストに追加していく result.push(point); } // 最終的にすべてのcardを追加したresultが、toPoint関数で変換したリストになる。 return result;
このような、「リストの各要素に対して関数を実行し、その結果を新しいリストに追加していく」という処理は、Haskellに限らず多くのプログラミング言語で頻繁に必要になります。 みなさんも、これとよく似た処理を、これまでに何度も書いてきたのではないでしょうか?
「よく似た処理」なら、抽象化して使いまわせる形にまとめられるはずです。
実際、上記のfor文をほかの似たような処理に使いたいときは、次の部分だけを書き換えればよさそうです。
// toPoint関数を実行した結果を、 point = toPoint(card);
この部分を書き換えられるように、上記のfor文でやっている処理を抽象化したのが、map関数だといえます。
Haskellはいわゆる「関数型プログラミング言語」であり、関数をファーストクラスオブジェクトとして扱えるので、
「toPoint関数を別の関数に差し替える」といったことが可能なのです。
関数をファーストクラスオブジェクトとして扱える言語はほかにも数多くあり、やはりmapという名前で同じ仕組みが提供されていることも多いので、親しみのある方も多いでしょう。
Haskellのmapを使い、手札の各カードに対して取り得る値をtoPointで計算するには、次のようにします。
$ stack ghci > :l blackjack.hs > map toPoint [A, N 2, J, N 3] [[1,11],[2],[10],[3]]
手札を表すリストと、その各要素であるカードの値の関係を図にすると、以下のようになっています。
[ A , N 2, J , N 3] ↓ ↓ ↓ ↓ [[1,11], [2] , [10], [3]]
リストの各要素をtoPoint関数の引数として渡し、実行した結果が、またリストに格納されたのが分かるでしょうか?
map関数を使うことで、「リストの各要素に対して関数(この例ではtoPoint)を実行する」というありふれたパターンを簡潔に実装できるのです。
letでローカル変数に関数の実行結果を保存する
前項では、map関数で手札に入った各カードから、取り得る値を計算しました。
次の処理を説明する前に、いったん計算結果をローカル変数に保存する方法を説明しておきましょう。
ローカル変数に保存することで、何度も同じ計算をするのを回避したり、ローカル変数として名前をつけることで意味を分かりやすくすることができるのは、Haskellでも同様です。
Haskellでローカル変数を定義する構文は2つあります。
今回はそのうちの1つ、letを紹介しましょう。
letは下記の形式で使用します。
let 変数名1 = ... 変数1の定義 ... 変数名2 = ... 変数2の定義 ... ... 変数名N = ... 変数Nの定義 ... in 定義した変数を使用する式
例で説明しましょう。
ただ、いままでのようにGHCiで試そうとしても、上記のような改行を含んだコードは入力できません。
GHCiで複数行の式を入力する場合は、:{ではじめて、:}で終えてください(なんだか顔文字みたいですね)。
GHCiに:{と入力してリターンキーを押すと、デフォルトではプロンプトが縦棒|に変わります。
この状態で、let ...で定義したい変数名と定義を列挙し、in以降でその変数を使用した式を書いてみてください。
下記の例のように、同じlet ...の中で定義した変数は、(in以降だけでなく)ほかの変数の定義においても参照できます。
> :{ | let x = 1 | y = x * 2 | in | x + y > :} 3
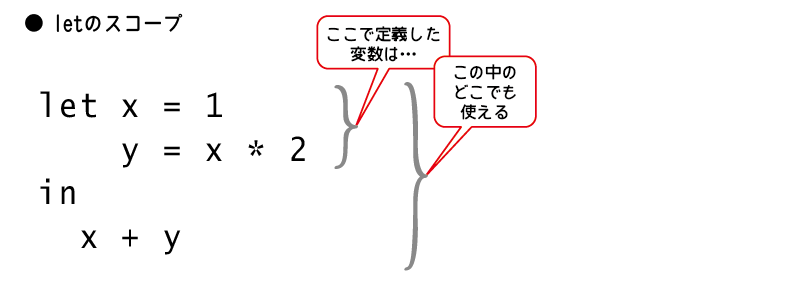
letで定義した変数が参照できる範囲
ちなみに、1行で書きたい場合はセミコロン;が使えます。
> let x = 1; y = x * 2 in y 2
sumHand関数でletを使い、手札の各カードにmapでtoPointした結果を保存してみましょう。
結果は「取り得る値のリスト」なので、possiblePointsという名前の変数に代入することにします。
sumHand :: [Card] -> Int sumHand cards = let possiblePoints = map toPoint cards ... さらなる途中の変数 ... in ...
ここから先は、「... さらなる途中の変数 ...」を作る方法について説明していきます。
foldl: 「これまでに処理した要素」の情報を使いながらリストを変換する
次に実装するのは「取り得る値すべてを組み合わせて、組み合わせごとに合計を求める」処理です。 とはいえ、このままだとちょっと複雑ですね。
処理の内容をさらに分解し、簡単そうな「合計を求める」の部分から考えてみることにしましょう。
単に「整数のリストの合計を求める」だけであれば、Haskellには標準でsum関数というのがあるので、それを使うだけです。
しかし、今回は「取り得る点数すべてを組み合わせて、組み合わせごとに」求めなければならないため、sum関数では単純すぎて役に立ちません。
そこで、手始めにsum関数を1から実装してみて、その過程をヒントにして目的の合計を求める関数へと発展させていく、というアプローチをとることにします。
sum関数の実装に使うのが、この節のタイトルにもなっているfoldl(「フォールド・エル」と読みます)関数です。
ほかのプログラミング言語にも、reduceやinjectという名前で似たような機能が用意されている場合があります。
foldl関数は、リストをさまざまな型の値に変換できる、万能関数です。
foldlを理解しておけば、リストを使う多くの場面で再帰関数を自力で書く必要がなくなります(foldlの代わりにfoldrなどの変種を使うこともありますが、それらの理解も簡単になります)。
foldlは、リストに何かを施すという点ではmap関数に似ています。
しかし、リストからリストへの変換に特化したmap関数に比べると、使用方法は少し複雑で、間違えたり可読性を下げたりするリスクも高くなります。
状況を見極めながら、なるべくmapなどの用途がより明確な関数を使用しましょう。
foldlの使い方
foldl関数は、次の形式で呼び出します。
foldl <関数> <初期値> <リスト>
map関数と同様、最後の引数である「リスト」は、各要素を処理したい対象のリストです。
<関数>は、mapに渡す関数と同様に、リストの各要素を受け取るのですが、それに加えて「それまでの<関数>の実行結果」も受け取ります。
具体的には、foldlの第1引数にくる関数は、次の形式で呼び出されるものです。
<関数> <それまでの実行結果> <リストの各要素>
この関数の2つ目の引数である<リストの各要素>は、文字通りfoldlに渡す<リスト>の各要素です。
では、1つ目の引数の<それまでの実行結果>とは何でしょうか?
この<それまでの実行結果>は、かみ砕いて言うと、「現在処理している<リストの各要素>より1つ前の要素を<関数>が処理したときの実行結果」という意味になります。
でも、「<リストの各要素>より1つ前の要素を処理した結果」ということは、リストの先頭の要素を処理するときはどうすればいいのでしょう?
その場合には「1つ前の要素」なんてありません。
そこで出てくるのが、foldl関数の第2引数である<初期値>です。
この<初期値>は、リストの先頭の要素に対して<関数>を実行する際、<それまでの実行結果>として<関数>の第1引数として渡されます。
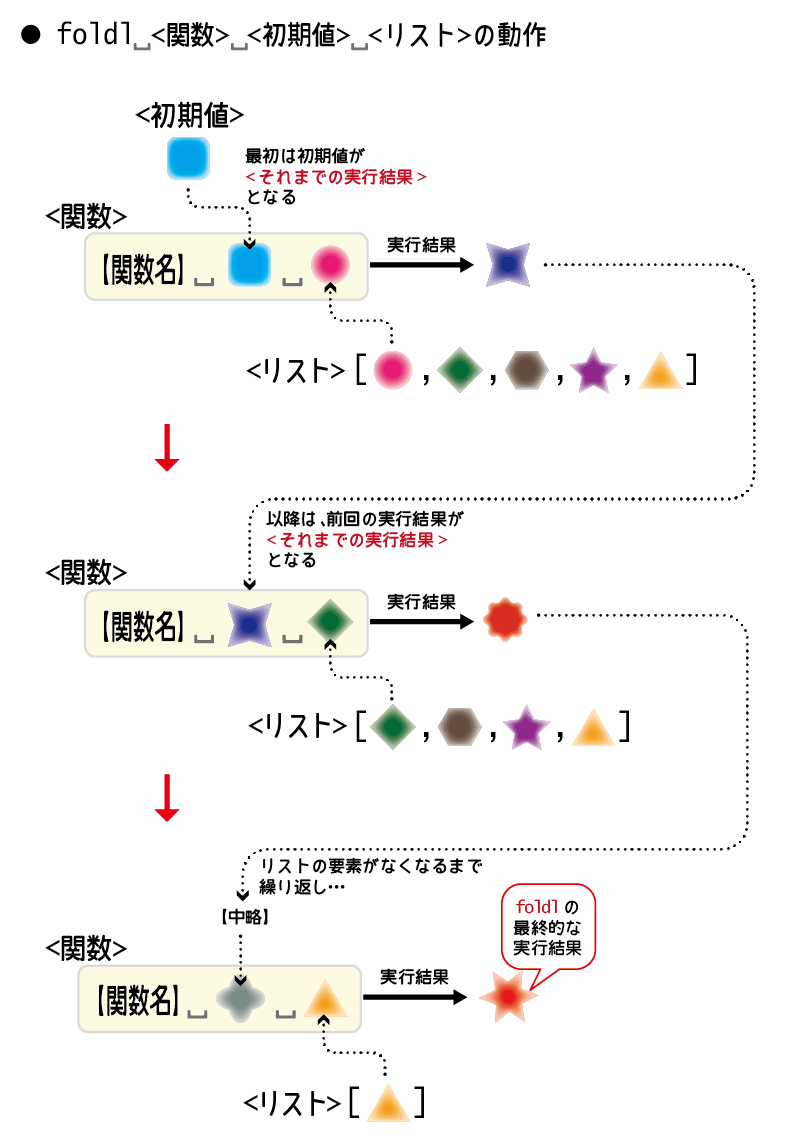
foldlはループの抽象化
【コラム】for文で理解するfoldl
foldlのような関数は、関数型プログラミングに慣れていないと、ちょっと分かりづらいかもしれません。
お馴染みのfor文で考えるとどうなるのか、疑似コードで見てみましょう。
function foldl(<関数>, <初期値>, <リスト>){
let <それまでの実行結果> = <初期値>;
for(<リストの要素> in <リスト>){
<それまでの実行結果> = <関数>(<それまでの実行結果>, <リストの要素>);
}
return <それまでの実行結果>;
}
foldlでやっていることは、「最終的な実行結果を初期化してから、ループを回してリストを1個ずつ処理し、最終的な実行結果を少しずつ組み立てていく」という、非常にありふれた実装パターンです。
この実装パターンを、「整数のリストを受け取って、その合計を求める関数」(つまりsum関数)に当てはめてみれば、よりそのことを実感できると思います。
上記のfor文バージョンのfoldlでsum関数を実装するには、<関数>には与えた2つの引数を足し合わせる関数、<初期値>には0を当てはめます。
let <それまでの実行結果> = 0;
for(<リストの要素> in <リスト>){
<それまでの実行結果> = <それまでの実行結果> + <リストの要素>;
}
return <それまでの実行結果>;
かなり見慣れたパターンに近づいてきたと思いませんか?
「<それまでの実行結果> = <それまでの実行結果> + <リストの要素>」の部分を、C言語などでよく使う+=演算子に置き換えると、さらにお馴染みの形になります。
let <それまでの実行結果> = 0;
for(<リストの要素> in <リスト>){
<それまでの実行結果> += <リストの要素>;
}
return <それまでの実行結果>;
sum関数もfoldl関数もないような状態で、プログラミング言語の標準APIだけでsumを1から実装することになった場合、おそらくはこのようなforループを書くことになるのではないでしょうか。
「最終的に結果となる変数をループの外で初期化してから、リストの要素を1つずつ取り出し、少しずつ変数を更新して、最終的な結果を作る」という、手続き型言語でもよく見るパターンを見事に抽象化しくれるのが、foldlなのです。
演算子を普通の関数として扱う
Haskellのfoldlを使って、sum関数を(再)実装してみましょう。
for文バージョンのコードでやったことを思い出しながらfoldl関数の引数として渡すと、次のように書き換えられます。
plus :: Int -> Int -> int plus x y = x + y sum :: [Int] -> Int sum list = foldl plus 0 list
foldl関数の引数は<関数>、<初期値>、<リスト>でした。
sum関数を実装するので、<初期値>は0、<リスト>はそのままsum関数が受け取るリストにすればいいですね。
<関数>は、「2つの引数を足し合わせる関数」ですので、そのような関数を別途定義して渡しています。
上記のコードで言うところのplus関数です。
Haskellでは、Boolや文字列、整数などと同様に、関数もそのまま引数として渡せるので、このように書いても何1つ問題はありません。
さて、とりあえず上記のように書いてみましたが、plus関数の定義を別に書かないといけないのは、ちょっと面倒ですよね。
なにか楽をする手はないでしょうか?
もちろん、あります! ☻
Haskellでは+のような演算子も、実はただの関数なのです(Rubyで+というメソッドが定義できるのと同じようなものですが、Haskellの場合、+、-、/、*のような記号だけでなく、もっといろいろな記号を組み合わせた関数も作れます。あまり頻繁に使うべきものではないですが)。
+も関数なので、当然、foldlの引数として渡せます。
ただし、構文が曖昧になってしまうので、そのまま+という記号は渡せません。
(+)という具合に、丸カッコで優しく包んであげましょう。
丸カッコで囲まれた(+)は、「第1引数として+の左辺を、第2引数として+の右辺を受け取る関数」となります。
試しにGHCiで下記のように実行してみてください。
> (+) 1 3 4
このように演算子を丸カッコで囲むと、ほかの普通の関数(「関数名 引数...」のように関数名を引数の前に置いて呼び出す関数)と同じように使えるようになります。
というわけで、foldl関数を使ったsum関数の定義は以下のように書き換えられます。
sum :: [Int] -> Int sum list = foldl (+) 0 list
余計な関数を定義する必要もなく、すっきり定義できましたね!
foldlやmapを使って、取り得るすべての合計点数を求める
さて、合計を求めるsum関数を定義することはできましたが、ゴールはそこではありませんでした
(そもそも、Haskellには標準でsum関数がありますしね)。
「カードが取り得る点数すべてを組み合わせて、組み合わせごとに合計を求める」のがいまの目標でしたね。
そのために必要な、foldlに渡す各引数の型と値をそれぞれ考えていきましょう。
まず<リスト>ですが、これはここまででmap関数を利用して得た、手札における各カードの取り得る値のリストです。
具体的には、letを使ってpossiblePointsという変数に代入したものです。
その各要素は、カードがAの場合は[1, 11]、3の場合は[3]といった具合に、Intのリストになっています。
従って、型としてはIntのリストのリスト、すなわち[[Int]]となります。
<初期値>については、foldlでリストの各要素を1つずつ使いながら最終的な実行結果を作るときに最初に使う値なので、
最終的な結果と同じ型でないといけません。
途中で型を変えることはできないのです。
いま最終的に欲しいのは「取り得る値の組み合わせごとの合計」なので、合計点数のリスト、すなわち[Int]という型にしましょう。
値として何を使えばいいかは、<関数>の値を検討する際に考えます。
最後に、一番難しい<関数>の部分です。
この<関数>が取る引数、すなわち<それまでの実行結果>と<リストの各要素>の型は、<リスト>と<初期値>が決まると自ずと決まります。
まず、<それまでの実行結果>ですが、これについては、「<初期値>は、リストの最初の要素に対して<関数>を実行する際、<それまでの実行結果>として<関数>の第1引数として渡される」という点を思い出してください。
<初期値>は<それまでの実行結果>の代わりになるのです。
こうした仕様のために、必然的に<それまでの実行結果>は<初期値>の型と同じ型、つまり今回の場合[Int]になります。
続いて、<リストの各要素>は、文字通りfoldlに渡す<リスト>の各要素です。
<リスト>の型は[[Int]]ですから、<リストの各要素>の型は[Int]となるのです。
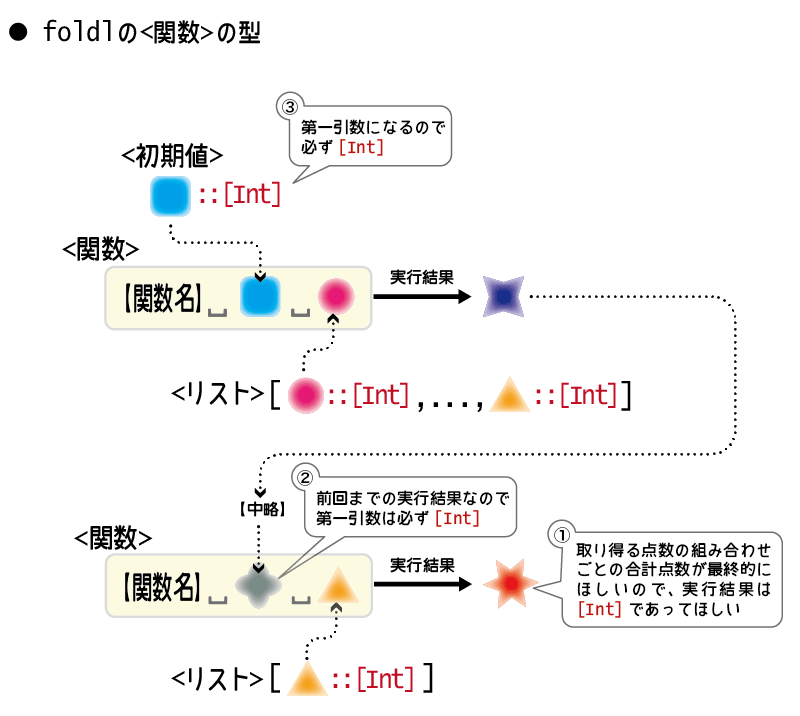
foldlに与える関数の型
以上の考察の結果、<関数>の型は下記のようになります。
:: [Int] -> [Int] -> [Int] -- ^^^^^ ^^^^^ ^^^^^ -- <それまでの実行結果> <リストの各要素> <最終的な実行結果>
ここまで分かったら、具体的な処理の内容を考えていきましょう。
単純に「合計を求める」ときの<関数>は、<それまでの実行結果>と<リストの各要素>を足し合わせるだけでよいのでした。
今度は、<それまでの実行結果>と<リストの各要素>のそれぞれがリストになっているため、それぞれを取り出してから足し合わせる必要があります。
「取り得る値すべてを組み合わせて、組み合わせごとに合計を求める」には、すべての組み合わせを総当たりで足し合わせなければなりません。
手札の中身が[A, A, A]だとすると、取り得る点数のリストは[[1, 11], [1, 11], [1, 11]]となるので、下図のような計算を行います。
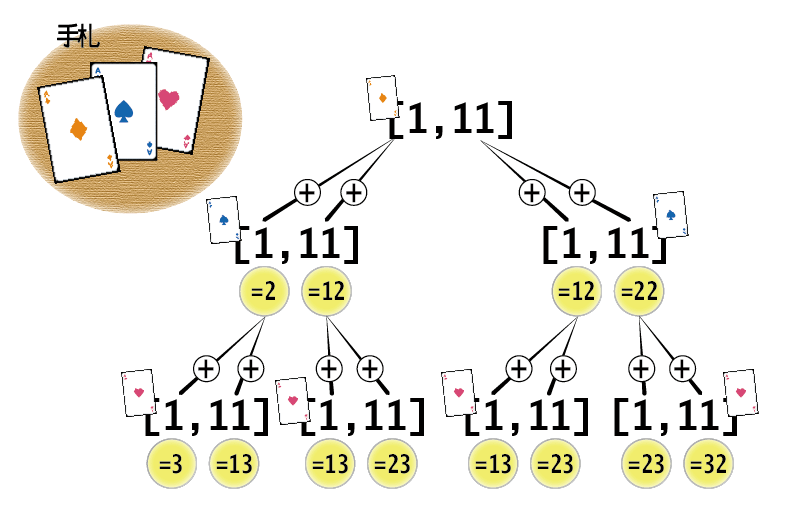
[A, A, A]の点数計算
図の中でイコール(=)の後ろに書かれた数が、各要素同士を足し算した結果です。
足し算の結果すべてを格納したリストが、<関数>が<それまでの実行結果>と<リストの要素>を計算した結果となります。
この図を見ると、「1つ目のA」の取り得る点数のリスト[1, 11]の各要素に対して、「2つ目のA」の取り得る点数のリスト[1, 11]の各要素を取り出し、それぞれを足し合わせていることが分かります。
ということは、下記のように2重のmap関数を使えば答えが出せそうです。
「リストの各要素に対して関数を実行する」というmap関数を、2つのリストに対して使用するのです。
この関数の名前はplusEachとしておきましょう。
plusEach list1 list2 = map (\element1 -> map (\element2 -> element1 + element2) list2) list1
\element1 ->という、見慣れない新しい構文が出てきましたね。
使い捨ての関数を定義する(ラムダ式)
\element1 -> ...や\element2 -> ...のように、バックスラッシュと細い右向きの矢印を使った構文は、「ラムダ式」といいます。
「mapなどの関数に渡す新しい関数を定義したい、でもそのためだけに新しい関数の名前を考えて変数に入れるのは面倒くさい」という場合に、使い捨ての関数を定義できるようにしてくれるのがラムダ式です。
ラムダ式の使用方法を一般化すると次のようになります。
(\仮引数名1 仮引数名2 ... 仮引数名N -> 関数の中身)
\から->までが、使い捨ての関数が受け取る仮引数名になります。複数の引数を受け取るラムダ式を定義したい場合は、仮引数名をそれぞれスペースで区切ります。
このラムダ式を使って定義したplusEach関数の中身を吟味しましょう。
map (\element1 -> map (\element2 -> element1 + element2) list2) list1
1つ目のmapに渡すラムダ式の中で、さらにmapを呼んでいます。
これによって、2つのリスト両方のそれぞれの要素を、総当たりで足し算しているわけです。
分かりやすくするために、改行とインデントを加えて、各部分に説明をコメントとして書き込んでみました。
plusEach list1 list2 = map (\element1 -> -- 1つ目のリストの各要素を、 map (\element2 -> -- 2つ目のリストの各要素と、 element1 + element2 -- 足し合わせる ) list2 ) list1
それぞれのmap関数で、list1とlist2のそれぞれの要素を1つずつ取り出し、足し合わせています。
map関数を二重に入れ子にすることで、「list1のすべての要素」におけるそれぞれに対して「list2のすべての要素」をそれぞれ処理できます。
なので、結果的に「すべての組み合わせ」を処理できるのです。
「リストのリスト」の入れ子を解く
いい感じに定義できているようなので、動作を確認してみましょう。
上記のplusEach関数をblackjack.hsに追記して保存して、またGHCiから:l blackjack.hsで読み込んでみましょう。
> plusEach [1, 11] [1, 11] [[2,12],[12,22]]
1 + 1、1 + 11、11 + 1、11 + 11という、すべての組み合わせについて合計を計算できていますね。
しかし、実際に返ってきた値は型がIntのリストのリスト、[[Int]]になってしまっています。
いま欲しい<最終的な実行結果>の型は、Intのリスト、つまり[Int]なので、これでは求めていたものになりません。
そこで、「リストのリスト」のような入れ子を一段解くための関数、concatを使います。
> concat (plusEach [1, 11] [1, 11]) [2,12,12,22]
これで欲しい型の値になりました!
さらにHaskellには、map関数が返した結果をconcatするという用途に特化したconcatMap関数というものもあります。
plusEach関数も、そのような形になっているので、concatMapを使って次のように書き換えておきましょう。
plusEach :: [Int] -> [Int] -> [Int] plusEach list1 list2 = concatMap (\element1 -> -- 1つ目のリストの各要素を、 map (\element2 -> -- 2つ目のリストの各要素と、 element1 + element2 -- 足し合わせる ) list2 ) list1
改めて動作確認してみましょう。
> plusEach [1, 11] [1, 11] [2,12,12,22]
バッチリですね!
型に合うfoldlの初期値を用意する
ここまでで、foldlに渡す引数<関数>、<初期値>、<リスト>のうち、<関数>と<リスト>を求めることができました。
残る<初期値>ですが、これは実際にそれらしい値を試してみると、どんな値が適切かが分かります。
これまでで触れたとおり、<初期値>の型は[Int]でした。
この[Int]は、最終的には「組み合わせごとの合計」になるので、「組み合わせごとの合計」がない状態、すなわち空のリストにするのがよいかも知れません。
ちょっとGHCiで試してみましょう。
> foldl plusEach [] [[1, 11], [1, 11], [3]] []
残念ながら、意図に反して空のリストが返ってきてしまいました。 なぜでしょう?
その理由は、map関数やconcatMap関数が、空のリストを受け取るとそのまま空のリストを返してしまうことにあります。
空のリストには引数となる要素がないので、関数の実行しがいがない、ということです。
これを回避するためには、<初期値>を空のリストにはせず、何かしら値の入ったリストにする必要があります。
空のリスト以外で「組み合わせごとの合計」がないリストは、ずばり0しか入っていないリスト、[0]です。
試してみましょう。
> foldl plusEach [0] [[1, 11], [1, 11], [3]] [5,15,15,25]
今度はちゃんと0 + 1 + 1 + 3、0 + 1 + 11 + 3、0 + 11 + 1 + 3、0 + 11 + 11 + 3というすべての結果を計算できました。
以上をまとめると、foldlに渡す引数は次のようになります。
foldl plusEach [0] possiblePoints
このfoldlで求めた「手札の各カードが取り得る値の、組み合わせごとの合計」も、letを使って変数に代入しておきましょう。
最終的な手札の合計点数の候補になるリストなので、scoreCandidatesという変数名にします。
そこまでを実装すると、sumHand関数の定義はここまで埋まります。
sumHand :: [Card] -> Int sumHand cards = let possiblePoints = map toPoint cards scoreCandidates = foldl plusEach [0] possiblePoints -- ... これから実装する ... in -- ... これから実装する ...
次は、候補の中からゲームのルールでより有利になる値を絞り込むことを考えます。
filter関数でバストしない合計点数のみを選ぶ
続いて実装するのは、「組み合わせから求めた合計のうち、バストしない(合計が21を超えない)もののみを選ぶ」処理です。
これを実現するには、filter関数を使うのがちょうどいいでしょう。
filter関数は、リストの各要素に対して関数を実行することで、リストの各要素を「選択」する関数です。
GHCiの:tコマンドで引数の型を見てみましょう。
> :t filter filter :: (a -> Bool) -> [a] -> [a]
filterも、map関数やfoldl関数と同様、第1引数として関数を受け取ります。
型宣言の中で(a -> Bool)のように丸カッコで囲まれている関数があれば、そこは関数型の値を受け取るのだと解釈してください。
filter関数に渡す関数は、aという型の値を受け取ってBool型の値、つまり真偽値を返さなければなりません。
このaは、何かそういう特定の型があるわけではなく、型変数と呼ばれるものです。
普通の型が大文字で始まる名前で表されるのに対して、型変数は必ず小文字で始まります。
型変数は任意の型を表していますが、「同じ文字で表される型変数は、同じ型でなければならない」というルールを覚えておいてください。
filter関数の型宣言に出てくる型変数はすべてaなので、何の型でもいいけれど、すべて同じ型でなければなりません。
このことから、filter関数が受け取る第一引数の関数(a -> Bool)は、リストの各要素aと同じ型である、ということが分かります。
[Int]が「Intのリスト」を表していたのと同じように、[a]は「とある型aのリスト」という意味になるのです。
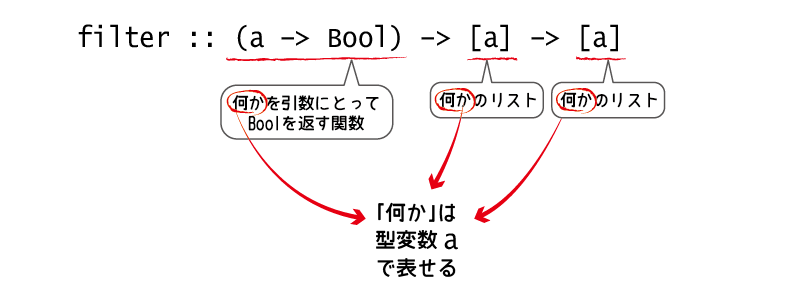
filterの型
filter関数の受け取る引数の型は分かりました。
では、filter関数が引数として受け取る(a -> Bool)の関数と、[a]のリストは、それぞれどういった値になるのでしょうか?
まず、[a]のリストは、要素を選択したいリストです。
(a -> Bool)の関数は、「filter関数はリストの各要素に対して関数を実行することで、リストの各要素を『選択』する関数」と述べたとおり、リストの各要素を「選択」するのに使用します。
具体的には、filter関数は(a -> Bool)の関数を実行して、True(真)を返した要素のみを選択します。
そして「選択」された((a -> Bool)の関数がTrueを返した要素のみの)リストが、filter関数の最終的な実行結果のリストとなるのです。
【コラム】手続き型言語で考えるfilter
filterも、手続き型言語の疑似コードを使って表現してみましょう。
(a -> Bool)のような関数は述語(predicate)と呼ばれることがあるのでpredicateという名前にし、[a]のリストはそのままlistとします。
// 結果を格納するための新しいリスト
result = [];
for(element in list){ // リストの各要素に対して
// predicate関数を実行した結果が、
bool = predicate(element);
if(bool){ // 真である場合のみ、
// 結果を格納するリストに追加していく
result.push(element);
}
}
// 最終的にpredicate(element)の結果がTrueになる要素だけが、
// 最終的な実行結果に含まれる。
return result;
このとおり、filter関数も、for文とif文を組み合わせた、ごくありふれたパターンの一般化なのです。
filter関数を利用して、「組み合わせから求めた合計のうち、バストしない(合計が21を超えない)もののみを選ぶ」処理を実装してみましょう。
まず、入力となるリストですが、これはもちろん前項でfoldlを使って計算したscoreCandidatesです。
関数については、今回はバストしない(合計が21を超えない)ものを選ぶことが目的なので、下記のような「合計が21以下であればTrueを返す」関数を使いましょう。
(\n -> n <= 21)
以上を合わせると、filter関数に次の引数を渡すことになります。
filter (\n -> n <= 21) scoreCandidates
ちょっと試してみましょう。
> filter (\n -> n <= 21) [1, 11, 23, 21, 22, 5] [1,11,21,5]
ちゃんと21を超えない合計だけのリストが返っていますね!
セクションでラムダ式を書かずに済ます
せっかくなので、上記の式をもっと簡潔かつ直感的に書く方法も知っておきましょう。
filter関数に渡していたラムダ式(\n -> n <= 21)に注目してください。
Haskellでは、セクションという機能を使うことで、ラムダ式を使わずに次のように短くできます!
(<= 21)
(\n -> n <= 21)の14文字から7文字まで削減できました。
圧縮率50%です!
セクションは、<=や+のような二項演算子から、左辺か右辺どちらか一方のみを渡した関数を簡単に作るのに使えます。
一般化すると(<演算子> <右辺の値>)あるいは(<左辺の値> <演算子>)という形式で使います。
これにより、ラムダ式の引数名や矢印などを書かなくてすむようになるんですね。
前に、+のような演算子を普通の関数として扱う方法を紹介しましたが、セクションはその記法を発展させたバージョンだと思ってください。
構文を曖昧にしないために、ここでも丸カッコが必要となります。
セクションのほかの例も挙げましょう。 GHCiに次のように入力してみてください。
> (/ 5) 13 -- (/ 5) で、「5で割る関数」になる 2.6 > (2 *) 109 -- (2 *) で、「2倍にして返す関数」になる 218
先ほどのfilter関数の呼び出しを、このセクションを使って書き直せば、次のようになります。
filter (<= 21) scoreCandidates
しつこいようですが、やはり値を入力して試してみましょう。
> filter (<= 21) [1, 11, 23, 21, 22, 5] [1,11,21,5]
振る舞いは変わらず、ちゃんと21を超えない合計のみが選ばれていますね!
このfilter関数で求めた「組み合わせから求めた合計のうち、バストしない(合計が21を超えない)もののみ」のリストをletを使って変数に代入するところまで実装すると、sumHand関数の定義はここまで埋まります。
sumHand :: [Card] -> Int sumHand cards = let possiblePoints = map toPoint cards scoreCandidates = foldl plusEach [0] possiblePoints noBust = filter (<= 21) scoreCandidates in -- ... これから定義する ...
「バストしない」もののリストなので、文字通りnoBustという名前の変数に保存しました。
値を返すifと値を返さない関数
残る処理は、下記の2つです。
- バストしない合計が1つでもあった場合、その中から最も高い値の合計を選んで返す
- バストしない合計が1つもない場合(どの合計もバストしてしまう)、合計の中から適当なものを選んで返す(ここでは「リストの先頭」を選ぶものとします)
「~場合」という日本語から推察できるように、上記の2つは条件分岐を使わなければ実装できません。
条件分岐といえばifですね。
ほかの多くのプログラミング言語と同様、Haskellでも条件分岐の構文としてifが使えます
(パターンマッチもある意味では条件分岐ですが、ここでは使用できません)。
Haskellのifは、if文とは呼ばれず、if式と呼ばれています。
Rubyなどのif式と同様に、「式」であるため、値を返します。
具体的には、次のような構文となっています。
if <条件> then <真の場合に返す値> else <偽の場合に返す値>
then <真の場合に返す値>とelse <偽の場合に返す値>と書かれていることからも分かるとおり、Haskellのifは値を返すのです。
else <偽の場合に返す値>が必須である点も、Haskellのif式ならではの特徴です。
なぜそんな制約があるのでしょう?
前回の記事で触れたように、Haskellにおける「純粋な関数」は、「引数を受け取って値を返す(ただし入出力処理などはできない)関数」です。
if式も、そうした純粋な関数と組み合わせて使う、ある意味純粋な関数なのです。
純粋な関数は、原則として、あらゆる場合を想定して対応した値を返さなければなりません。
if式もそうしたルールに準拠しているため、<条件>がTrueを返す場合とFalseを返す場合の両方を想定しているのです。
この「純粋な関数は、原則として、あらゆる場合を想定して対応した値を返さなければならない」というルールは、この後の説明でも言及するので覚えておいてください。
ifの条件
いまif式を使って場合分けしたいのは、「バストしない合計が1つでもあった場合」と「バストしない合計が1つもない場合」です。
これまでに使用したmap関数、foldl関数、filter関数などによって、「組み合わせから求めた合計のうち、バストしない(合計が21を超えない)もの」のリストがnoBustという変数に代入されています。
このnoBustというリストが空であるか、あるいは1つ以上の要素を持つかによって、場合分けをすればよさそうです。
リストが空であるか調べるには、nullという関数を使いましょう
(ちょっと変わった名前ですね)。
null関数は、空のリストを渡すとTrue、空でないリストを渡すとFalseを返します。
> null [] True > null [1] False
null関数とif式を使って、リストnoBustが空かどうかで場合分けするところまでsumHand関数を実装してみましょう。
sumHand :: [Card] -> Int sumHand cards = let possiblePoints = map toPoint cards scoreCandidates = foldl plusEach [0] possiblePoints noBust = filter (<= 21) scoreCandidates in if null noBust then <組み合わせから求めた合計から、適当なものを取り出す> else <最も高い値の合計を選ぶ>
sumHandの完成までもう少しですね!
thenの処理
残りの処理についても一気に実装してしまいましょう。
まずは、then節の<組み合わせから求めた合計から、適当なものを取り出す>処理です。ここで「組み合わせから求めた合計」というのは、foldl関数を使って足し合わせて作ったscoreCandidatesのことでした。
そして、「適当なものを取り出す」処理は、ひとまずscoreCandidatesの先頭の要素ということにします。
どの要素を取り出してもいいのですが、Haskellのリストから要素を取り出すときに最も簡単に取り出せるのは先頭の要素なので、先頭の要素としました。
リストの先頭の要素を取り出すには、文字通りheadという関数を使います。
つまり、これをscoreCandidatesに対して実行したhead scoreCandidatesという式が<組み合わせた合計点数から、適当なものを取り出す>処理の実装となります。
elseの処理
最後の<最も高い値の合計を選ぶ>処理は、maximum関数という、これまた文字通りな名前の関数を使えば実装できます。
「バストしない合計が1つでもあった場合、その中から最も高い値の合計を選んで返す」というのがelse節で行うべき処理なので、filter関数で作った、noBustというリストがその対象となります。
なのでmaximum noBustが<最も高い値の合計を選ぶ>処理に当たります。
【コラム】値を返さない関数に注意
以上をまとめる前に、ここで紹介した、head関数とmaximum関数に共通する、非常に重要な注意点を述べておきましょう。
なんと、この2つの関数は、「値を返さない」ことがあるのです。
先ほどif式の説明で、「純粋な関数は、原則として、あらゆる場合を想定して対応した値を返さなければなりません」と言っていたのに、これはどういうことでしょう?
残念ながら、Haskellの世界には、標準で使える関数の中にこのルールを破ってしまっているものがいくつかあります。
そのうちの2つがhead関数とmaximum関数なのです。
それぞれ、どういう場合に値を返さないのか、先へ進む前に想像してみてください。 GHCiでいろいろ試してみるのもいいでしょう。
分かりましたか?
それでは答えを言いましょう。
答えは、head関数とmaximum関数ともに、「空のリストを受け取った場合」です。
> head []
*** Exception: Prelude.head: empty list
> maximum []
*** Exception: Prelude.maximum: empty listExceptionと書かれたメッセージが出力されました。
これは、文字通り、Haskellにおける「例外」です。
head関数とmaximum関数は、いずれもリストから何らかの要素を1個取り出す関数です。
それぞれ、先頭の要素および最も高い値の要素ですね。
しかし、空のリストには要素がないので、いずれの関数でも取り出すことができません。
これがhead関数とmaximum関数が「値を返さない」場合になります。
「値を返さない」場合、Haskellの関数は(文字通り)例外を投げます。
この「例外」は、ほかのプログラミング言語における例外と概ね似ています。
プログラムの実行中に何らかの関数から例外が投げられてしまった場合、catchなどの関数で処理しない限り、プログラムがそのまま強制終了してしまいます。
こうした事態は極力避けたいものですよね。
SwiftやKotlin、Scalaなど、最近の静的型付けのプログラミング言語では、プログラムの強制終了を確実に回避しながら、関数が「値を返さない」場合を処理するための型が提供されています。
Optionalと呼ばれる型です。
もちろんHaskellにもそうしたOptionalのような型があります
Haskellにおけるそのような型は、Maybe型といいます。
これらの型は、直和型が持つ「値コンストラクターが特定のものの場合だけプロパティを保持できる」という性質を生かして、「値を返さない」場合の値コンストラクターと、「値を返す」場合の値コンストラクターとで分けることにより、型の利用者が「値を返さない」場合を必ず想定するように作られています。
「値を返さない」場合を、利用者が必ず想定できるようにすることによって、例外(すなわちプログラムの強制終了)を確実に回避できるのです。
そうした便利な道具があるにもかかわらず、headやmaximumは歴史的な事情により、「値を返さない」場合に例外を投げてしまいます。
ですので、「絶対にこのリストは空じゃない」ということが分かっている場合、例えば今回のように事前にnull関数でリストが空かどうかチェックしている場合にのみ使うようにしましょう。
head関数とmaximum関数の注意事項が分かったところで、いよいよそれらを使ってsumHand関数の実装をすべて埋めましょう。
次のような定義となります。
sumHand :: [Card] -> Int sumHand cards = -- 手札の各カードから取り得る点数を計算し、 let possiblePoints = map toPoint cards -- 取り得る点数すべてを組み合わせて、組み合わせごとに合計を求める scoreCandidates = foldl plusEach [0] possiblePoints -- 組み合わせた合計点数のうち、 -- バストしない(合計点数が21点を超えない)もののみを選ぶ noBust = filter (<= 21) scoreCandidates in -- バストしない合計点数が1つもないか調べて、 if null noBust -- バストしない合計点数が1つもない場合場合、 -- 組み合わせた合計点数から、適当なものを取り出す then head scoreCandidates -- バストしない合計点数が1つでもあった場合、 -- その中から最も高い点数のものを選んで返す else maximum noBust
すべての内容を丁寧に解説したので、説明はかなり長くなりましたが、出来上がった関数はこんなに短く、しかも意図が明確に分かるコードとして書けました!
まとめと次回予告
今回の記事では、アプリケーションの一部を書きながらHaskellの基本的な機能をかなり詳しく説明しました。
問題を表現する型を自分で定義し、その型を利用する関数をmapやfoldlなどの高階関数を使って定義していくのは、実際にHaskellプログラマーがアプリケーションを書くときの典型的なアプローチです。
次回は「型の応用編」として、sumHand関数を再定義してリファクタリングし、さらに安全なものにしていきます。
加えて、より深くHaskellプログラミングを学ぶためのガイドとなる情報をお伝えする予定です!
発展編! Haskellで「型」のポテンシャルを最大限に引き出すには?【第二言語としてのHaskell】
執筆者プロフィール
山本悠滋(やまもと・ゆうじ) 


編集協力:鹿野桂一郎(しかの・けいいちろう、





